Longitudinal Enlargement - Computation & Meaning

CommonRoad-Reach
1

My understanding

The reachable sets are positions that the rear axle (or center) can reach. When computing the collision free reachable sets, we must ensure that not only it, but also the front (and back) of the car does not collide with any obstacles, hence the enlargement part. What makes the task more difficult is that the amount of enlargement needed is highly dependent on the reference path and the vehicle’s distance to it, as we are working in curvilinear coordinates. I have tried to sketch that below, assuming a kinematic bicycle model. I haven’t done anything similar in a while, so please correct me if I’m wrong. I have used

  • L - wheelbase length
  • r - turning radius of reference path
  • s - distance from reference path, <0 when on “inside”, >0 when on “outside” of the turn

To me it seems sufficient to compute $\alpha=atan(\frac{L}{r+s})$. The enlargement E should then be $E=\alpha r$.

image
image1920×2560 289 KB

Please excuse my ugly (slightly incorrect) sketch.

Questions

  1. How is the lookup table computed?
  2. Why is it required? I can’t see any large gains in terms of computational efficiency with my current understanding.
2

Hi Boyanh,

you can find more details about the enlargement computation in the appendix of this article.

1 Like
3

Hi Edmond, thanks for the reference!

As I understand, the used method for computing the enlargement for a single position is quite similar to what I imagined. What I don’t understand is

Set of Positions: For computational efficiency, we overapproximate (11) for a set of positions…

But computing (11) and (12) doesn’t seem much more computationally expensive that finding the right values in the lookup table.

In the current approach, the largest (worst-case) enlargement anywhere on the reference path is used everywhere, given the same lateral distance s. So if there is a tight curve anywhere on the path, large enlargement values would be computed. Did you have any problems with that in realistic scenarios?

4

Hi Boyan,

In the current approach, the largest (worst-case) enlargement anywhere on the reference path is used everywhere, given the same lateral distance s . So if there is a tight curve anywhere on the path, large enlargement values would be computed.

The max/min curvature values taken into account for the enlargement are retrieved from the longitudinal range of each individual base reachable set. I.e., if one has a reference path with a tight curve, the high curvature would only affect those sets for enlargement purposes whose longitudinal coordinates lie in the vicinity of the tight curve. See here, where curvatureRange() retreives max/min curvature within a longitudinal interval.

Hope this answers your question. Don’t hesitate to reach out if you have any further questions.

Best,
Gerald

1 Like
5

Hi Gerald,

thanks for pointing that out! I must have been blind yesterday and completely missed it. With that, I think the approximation is not too conservative at all, it’s actually quite elegant :+1:

I now looked at the precomputed values in the lookup table. Are you sure these are correct?

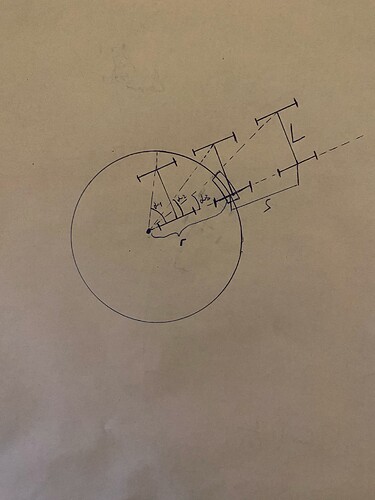
Intuitively, and looking at the sketch above or the one in the paper, I would expect the maximum enlargement to never exceed a quarter of a turning circle’s arc. The worst (largest) case would be when the rear axle is almost at the center of the turning circle. Any positions beyond that are not in the projection domain at all and should not be considered. So how can taking the maximum of many such computations [if I understand (13) correctly] can ever lead to such big values?

Let’s look at this single example from one of the tables.

s       = 2.77310924369748
k_min   = 0.198480355819125
k_max   = 0.209507042253521
l       = 2.6  # Wheelbase length, table is lut_ref_rear_wheelbase_26.txt, so 2.6m
result  = 14.4378501602189

Computing (11) from the paper for k_min and k_max yields 4.303252392058647 and 4.367875612725284 respectively. I wasn’t aware that (11) isn’t monotonic w.r.t the curvature, I would intuitively expect it to be. I didn’t read on [76], but instead created a small script to expand the range between k_min and k_max, compute (11) and take the maximum. No matter how many values I used, the result was still 4.367875612725284.

Best regards,
Boyan

I can’t upload a notebook, so I’m copying its markdown here.

import math

# From example, see link
s       = 2.77310924369748
k_min   = 0.198480355819125
k_max   = 0.209507042253521
l       = 2.6  # Wheelbase length, table is lut_ref_rear_wheelbase_26.txt, so 2.6m

def get_enlargement(l, s, k):
    """
    Computes (11)
    """
    r = 1 / k
    alpha = math.atan(l / (r-s))
    return alpha * r

get_enlargement(l, s, k_min), get_enlargement(l, s, k_max) 

(4.303252392058647, 4.367875612725284)

def yield_values_in_range(start, stop, n_values=1000):
    """
    Yields n_values successive values in the range [start, stop] 
    """
    
    # allow passing scientific notation
    n_values = int(n_values)
    
    diff = stop - start
    step_size = diff / (n_values-1)
    yield from (
        start + i*step_size
        for i in range(n_values)
    )

list(yield_values_in_range(1, 2, n_values=11))

[1.0, 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7000000000000002, 1.8, 1.9, 2.0]

def get_enalrgement_in_range(l, s, k_min, k_max, n_values=1e6):
    """
    Computes (13) in an inefficient manner
    """

    return max(
        (
            get_enlargement(l, s, k)
            for k in yield_values_in_range(k_min, k_max, n_values=n_values)
        )
    )

%%time
get_enalrgement_in_range(l, s, k_min, k_max, 2)

CPU times: user 6 µs, sys: 1 µs, total: 7 µs
Wall time: 8.34 µs





4.367875612725284

%%time
get_enalrgement_in_range(l, s, k_min, k_max, 1e6)

CPU times: user 145 ms, sys: 234 µs, total: 146 ms
Wall time: 145 ms





4.367875612725284

%%time
get_enalrgement_in_range(l, s, k_min, k_max, 1e7)

CPU times: user 1.42 s, sys: 278 µs, total: 1.42 s
Wall time: 1.42 s





4.367875612725284

%%time
get_enalrgement_in_range(l, s, k_min, k_max, 1e8)

CPU times: user 14.3 s, sys: 18 µs, total: 14.3 s
Wall time: 14.3 s





4.367875612725284